Vélnámi með viðgjafaraðferð1 má skipta í tvær tegundir vandamála. Annars vegar aðhvarfsvandamál2, og hins vegar flokkunarvandamál3. Í þessari færslu ætla ég að vinna mig í gegnum flokkunarvandamál, þar sem áherslan verður á að skoða forvinnsluaðgerðir4. Æfingin er fengin úr þriðja kafla bókarinnar Applied Predictive Modeling eftir Max Kuhn og Kjell Johnson. Nánar tiltekið er þetta verkefni 3.1.
Flokkum gler
Í þessu fyrsta vandamáli okkar í vélnámi notumst við við gagnasett úr The UC Irvine Machine Learning Repository sem snýr að greiningu mismunandi tegunda glers út frá ljósbrotsstuðli og samspili 8 mismunandi frumefna: Na, Mg Al, Si, K, Ca, Ba og Fe. Ljósbrotsstuðullinn og frumefnin eru skýribreyturnar og svarbreytan er tegund glersins. Sumsé, við viljum geta búið til líkan þannig að ef við höfum mælingar fyrir frumefnin og ljósbrotsstuðulinn getum við spáð fyrir um hvaða flokki þetta gler tilheyrir. Helst með þokkalegri nákvæmni.
Við nálgumst gögnin í mlbench pakkann, en auk hans hlöðum við inn öðrum pökkum sem við munum nota við úrvinnslu verkefnisins.
library(mlbench)
library(AppliedPredictiveModeling)
library(tidyverse)
library(tidymodels)
library(corrplot)
library(caret)
library(caretEnsemble)
library(viridis)
library(doParallel)
library(janitor)Nú þegar við höfum hlaðið inn mlbench pakkanum getum við sótt Glass gögnin með data() aðgerðinni og skoðum strúktúr gagnanna með str() fallinu.
data(Glass)
str(Glass)## 'data.frame': 214 obs. of 10 variables:
## $ RI : num 1.52 1.52 1.52 1.52 1.52 ...
## $ Na : num 13.6 13.9 13.5 13.2 13.3 ...
## $ Mg : num 4.49 3.6 3.55 3.69 3.62 3.61 3.6 3.61 3.58 3.6 ...
## $ Al : num 1.1 1.36 1.54 1.29 1.24 1.62 1.14 1.05 1.37 1.36 ...
## $ Si : num 71.8 72.7 73 72.6 73.1 ...
## $ K : num 0.06 0.48 0.39 0.57 0.55 0.64 0.58 0.57 0.56 0.57 ...
## $ Ca : num 8.75 7.83 7.78 8.22 8.07 8.07 8.17 8.24 8.3 8.4 ...
## $ Ba : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Fe : num 0 0 0 0 0 0.26 0 0 0 0.11 ...
## $ Type: Factor w/ 6 levels "1","2","3","5",..: 1 1 1 1 1 1 1 1 1 1 ...Við sjáum að Glass er gagnarammi með 214 athugunum á 10 breytum. Þar af eru níu talnabreytur og ein flokkabreyta. Flokkabreytan er svarbreytan okkar, þ.e. tegundir glersins, og eru 6 mismunandi tegundir.
Nú skulum við vinda okkur í verkefnin.
Leiðbeiningarnar eru eftirfarandi
- Using vizualisations, explore the predictor variables to understand their distributions as well as the relationships between predictors
- Do there appear to be any outliers in the data? Are any predictors skewed?
- Are there any relevant transformations of one or more predictors that might improve the classification model?
Eins og svo oft er ef til vill best hér að byrja með tíðniriti eða þéttniriti til að sjá dreifingu gilda innan hverrar skýribreytu. Við gerum eitt þéttnirit og eitt boxplott.
#Þéttnirit
Glass %>%
gather(-Type, key = "efni", value = "gildi") %>%
ggplot(mapping = aes(x = gildi)) +
geom_density() +
facet_wrap(~efni, scales = "free")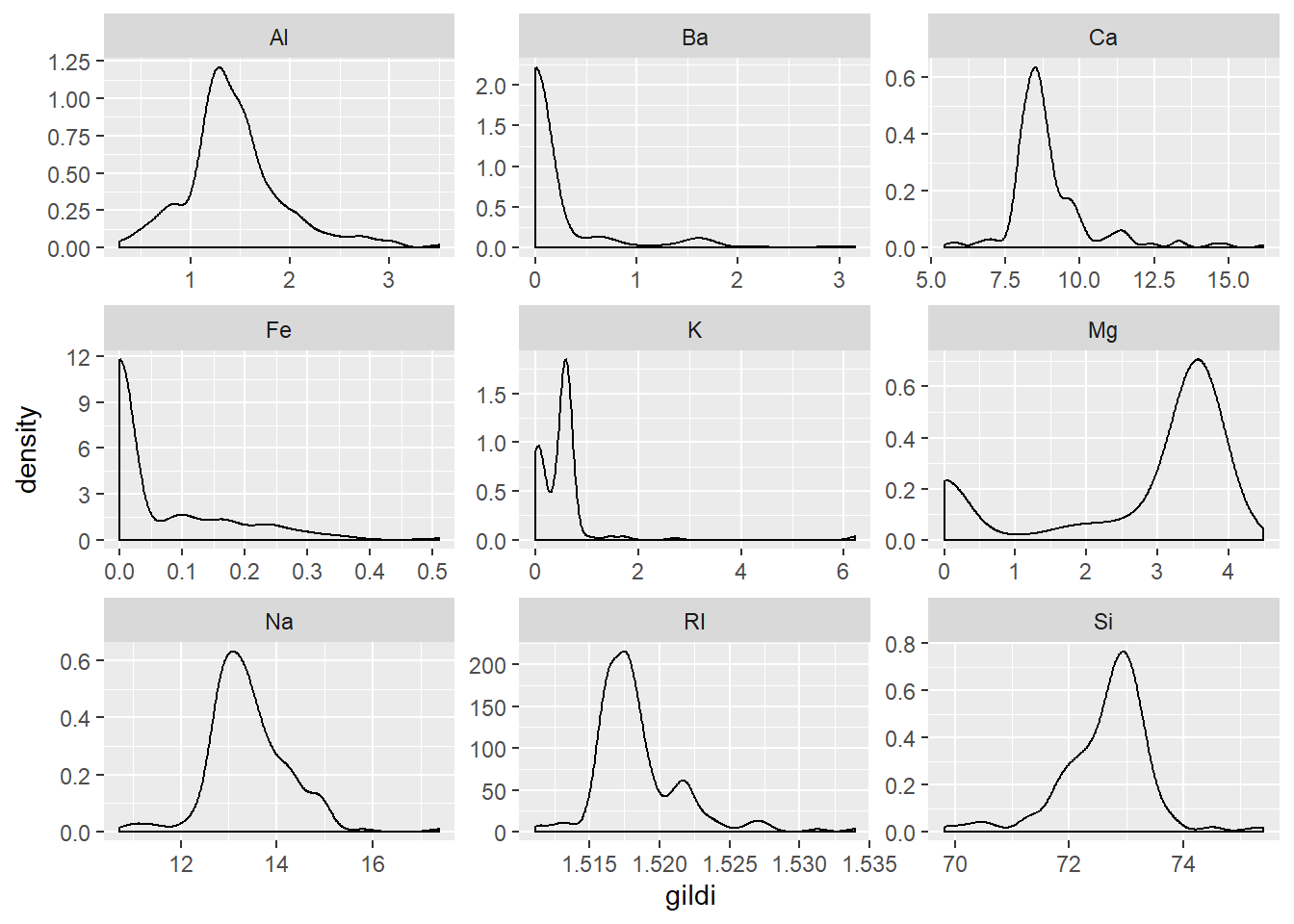
#Boxplott
Glass %>%
gather(-Type, key = "efni", value = "gildi") %>%
ggplot(mapping = aes(x = efni, y = gildi)) +
geom_boxplot()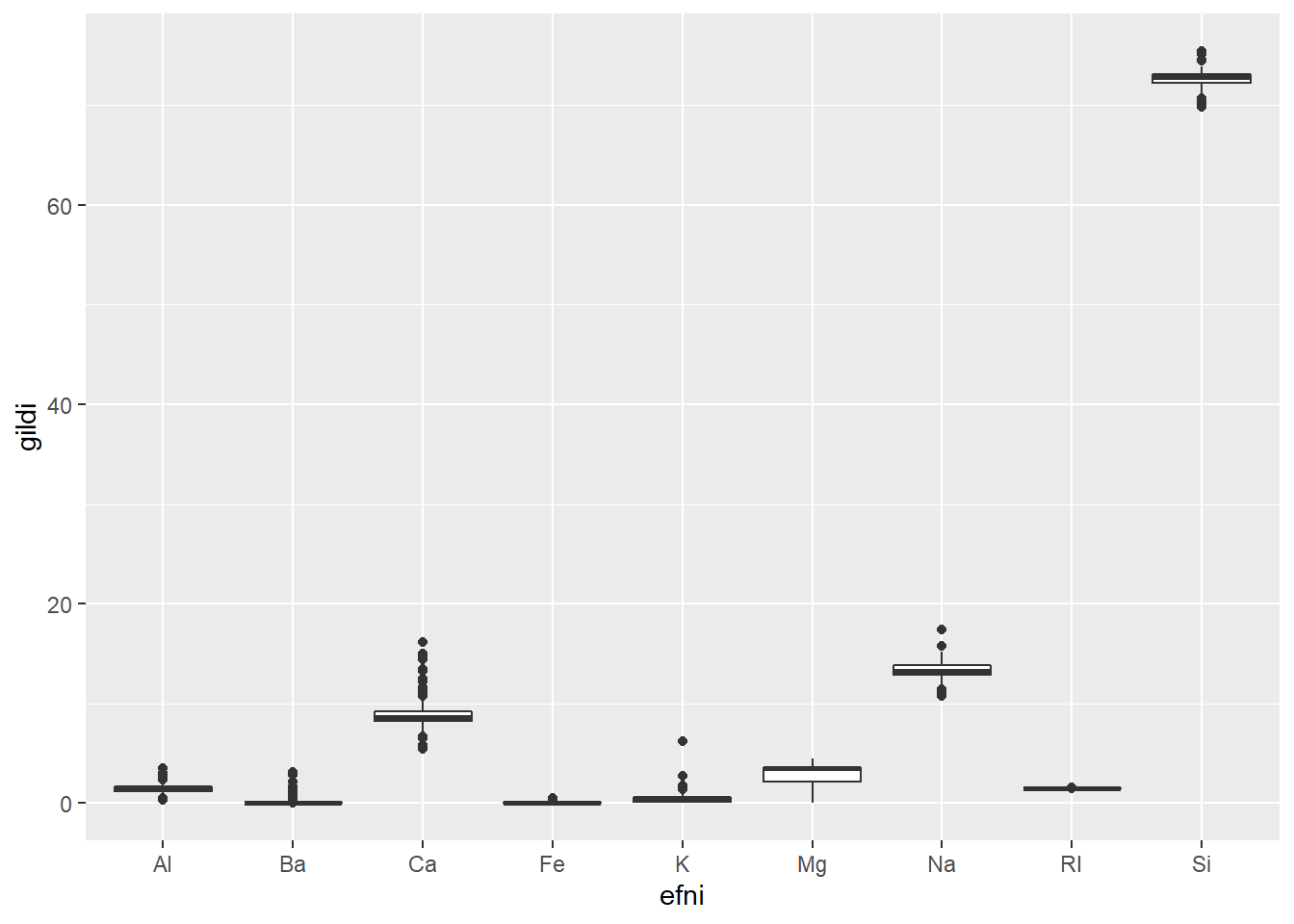
Við sjáum að þónokkur skekking er til staðar fyrir efnin Ba, Ca, Fe og ljósbrotsstuðulinn RI. Auk þess eru K og Mg tvítoppa. Þá virðist vera nokkuð afgerandi útlagi í K.
Því næst skoðum við fylgnirit milli skýribreytanna og notum til þess corrplot pakkann sem við höfum nú þegar hlaðið inn. Röðun breytanna á plottinu er fengin með hclust klösunarreikniriti.
#Skilgreinum hvaða dálkar innihalda skýribreytur svo hægt sé að vísa til þeirra með nafni
skyribreytur <- names(Glass)[1:9]
#Til að laga corrplot er merkingum ása leyft að fara yfir spássíur með eftirfarandi breytingu
par(xpd = TRUE)
#Fylgniplott
fylgni <- cor(Glass[, skyribreytur])
corrplot(fylgni, method = "square", mar = c(1, 1, 1, 1), order = "hclust")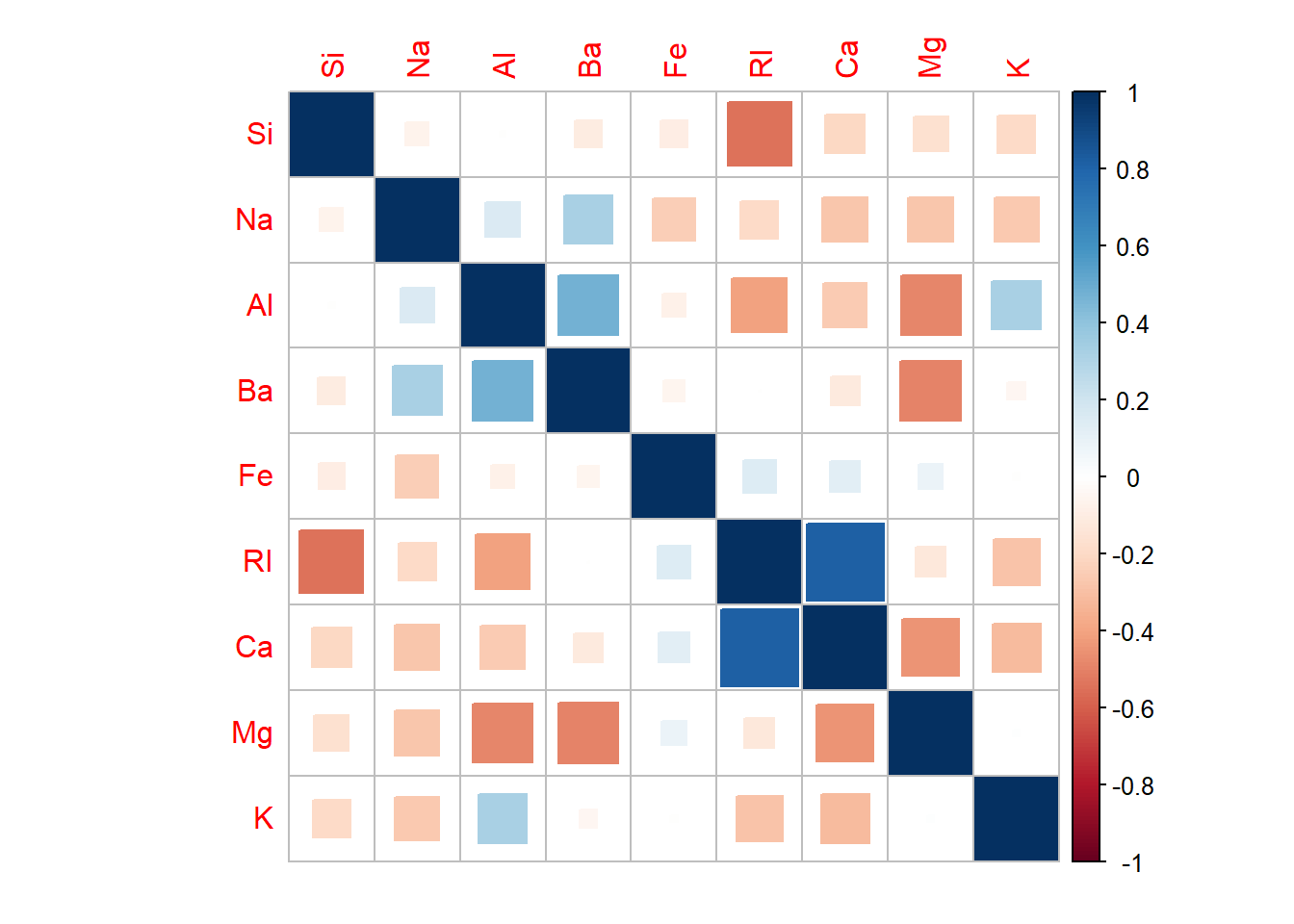
Við sjáum strax að það er eitthvað um fylgni milli skýribreyta. Sterkust er greinilega jákvæð fylgni milli ljósbrotsstuðulsins RI og svo Ca og þvínæst neikvæð fylgni milli ljósbrotsstuðulsins RI og Si. Marglínuleiki (fylgni milli skýribreytanna) getur valdið vandræðum í hinum ýmsu líkönum og þá skiptir ekki máli hvort fylgnin sé neikvæð eða jákvæð. Til frekari glöggvunar setjum við fram fylgnina á tvo aðra vegu, með hitakorti og súluriti.
fylgni_df <- as_tibble(fylgni) %>%
mutate(names = rownames(fylgni)) %>%
gather(-names, key = "key", value = "Fylgni") %>%
mutate(var_1 = pmin(names, key), # Setjum breytuna sem er á undan í stafrófinu í dálkinn var_1
var_2 = pmax(names, key)) %>% # og breytuna sem er á eftir í stafrófinu í dálkinn var_2
distinct(var_1, var_2, Fylgni) # og er hægt að ná í einstakar samsetningar með distinct
#Hitakort
fylgni_df %>%
mutate(Fylgni = if_else(var_1 == var_2, NA_real_, Fylgni)) %>%
ggplot(mapping = aes(x = var_1, y = var_2, fill = abs(Fylgni))) +
geom_tile() +
scale_fill_viridis()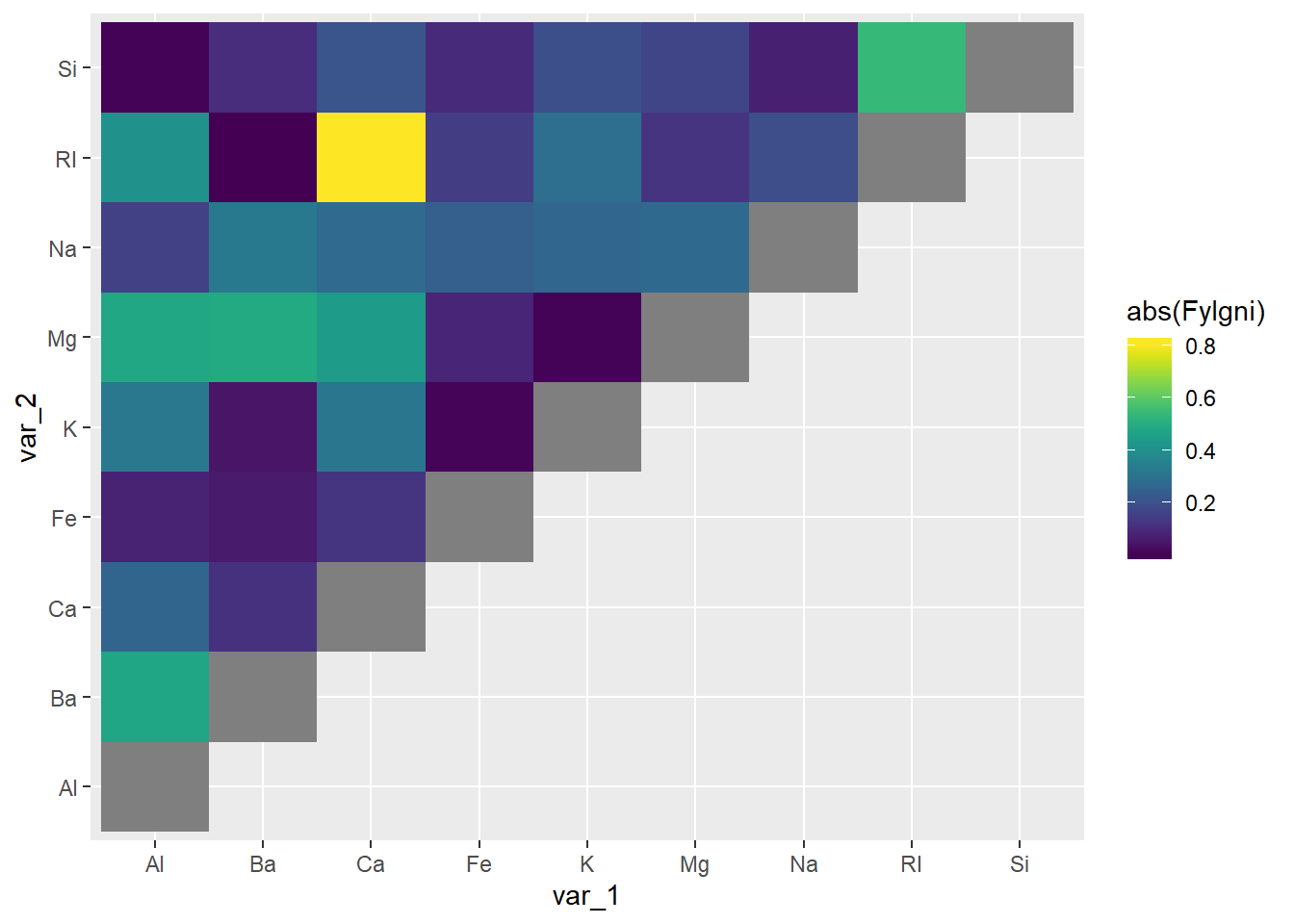
fylgni_df_utd <- fylgni_df %>%
filter(var_1 != var_2) %>% # Fjarlægjum fylgni breytu við sjálfa sig
arrange(Fylgni) %>%
unite(var_1, var_2, sep = "/", col = "Efni")
nota_palette <- c("#bbbbbb", "#F8766D", "#00BFC4")
throskuldur <- 0.32
#Súlurit
fylgni_df_utd %>%
mutate(Skipting = case_when(Fylgni > throskuldur ~ "Tiltölulega sterk jákvæð fylgni",
Fylgni < -throskuldur ~ "Tiltölulega sterk neikvæð fylgni",
TRUE ~ "Minni fylgni")) %>%
ggplot(mapping = aes(x = as.numeric(rownames(.)), y = Fylgni, fill = Skipting)) +
geom_bar(stat = "identity") +
scale_x_continuous(breaks = NULL, labels = NULL, name = "Samsetningar") +
scale_fill_manual(values = nota_palette) +
geom_hline(yintercept = 0)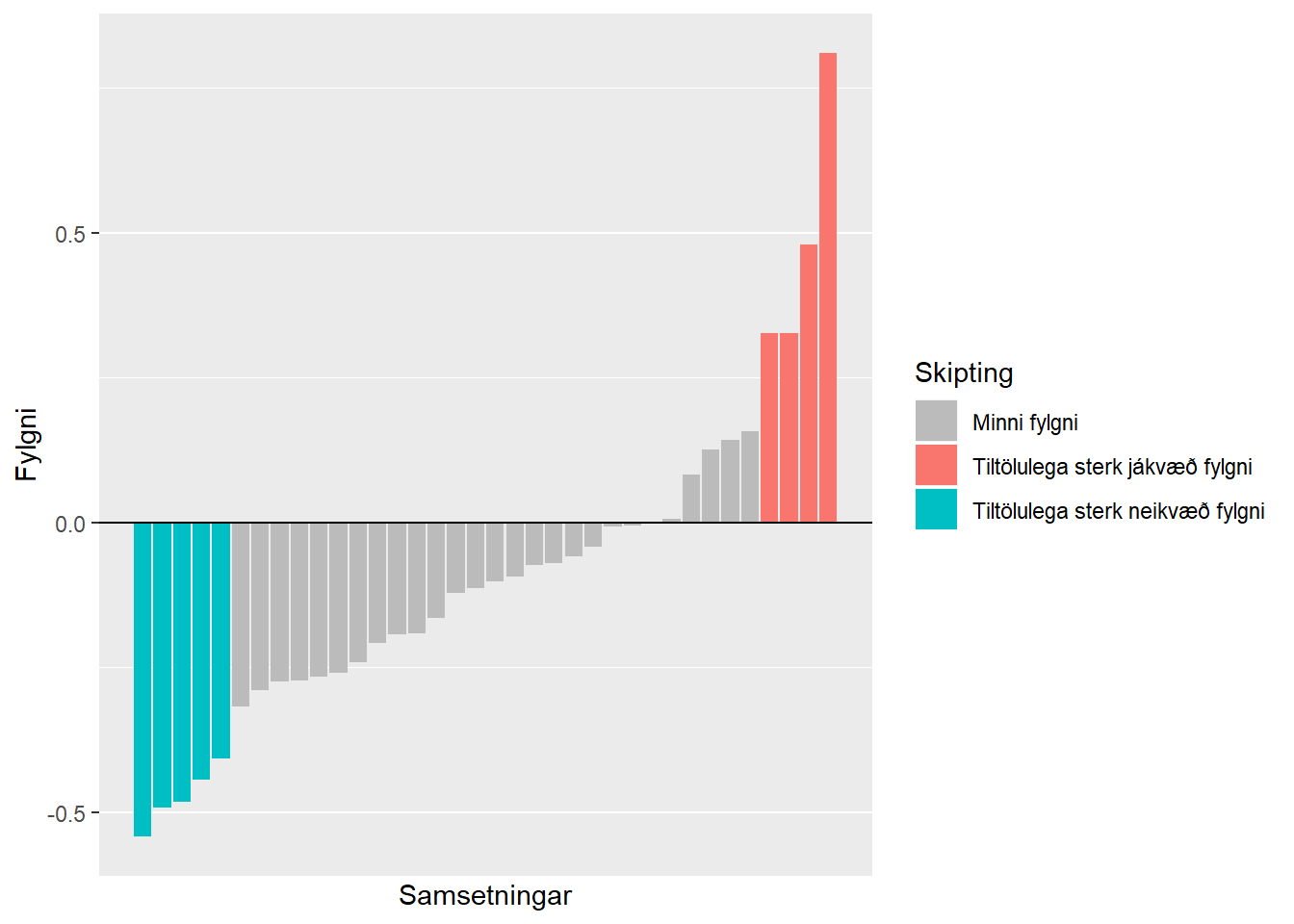
#Súlurit frh.
fylgni_df_utd %>%
filter(abs(Fylgni) > 0.32) %>% # Fjarlægjum fylgni sem er ekki meiri en +- 0.32
mutate(Formerki = if_else(Fylgni >= 0, "Jákvætt", "Neikvætt")) %>%
ggplot(mapping = aes(x = as.numeric(rownames(.)), y = Fylgni, fill = Formerki)) +
geom_bar(stat = "identity") +
geom_text(mapping = aes(label = Efni, vjust = if_else(Fylgni > 0, -0.9, 1.6))) +
scale_x_continuous(breaks = NULL, labels = NULL, name = "Samsetningar") +
geom_hline(yintercept = 0) +
coord_cartesian(ylim = c(-0.6, 0.9))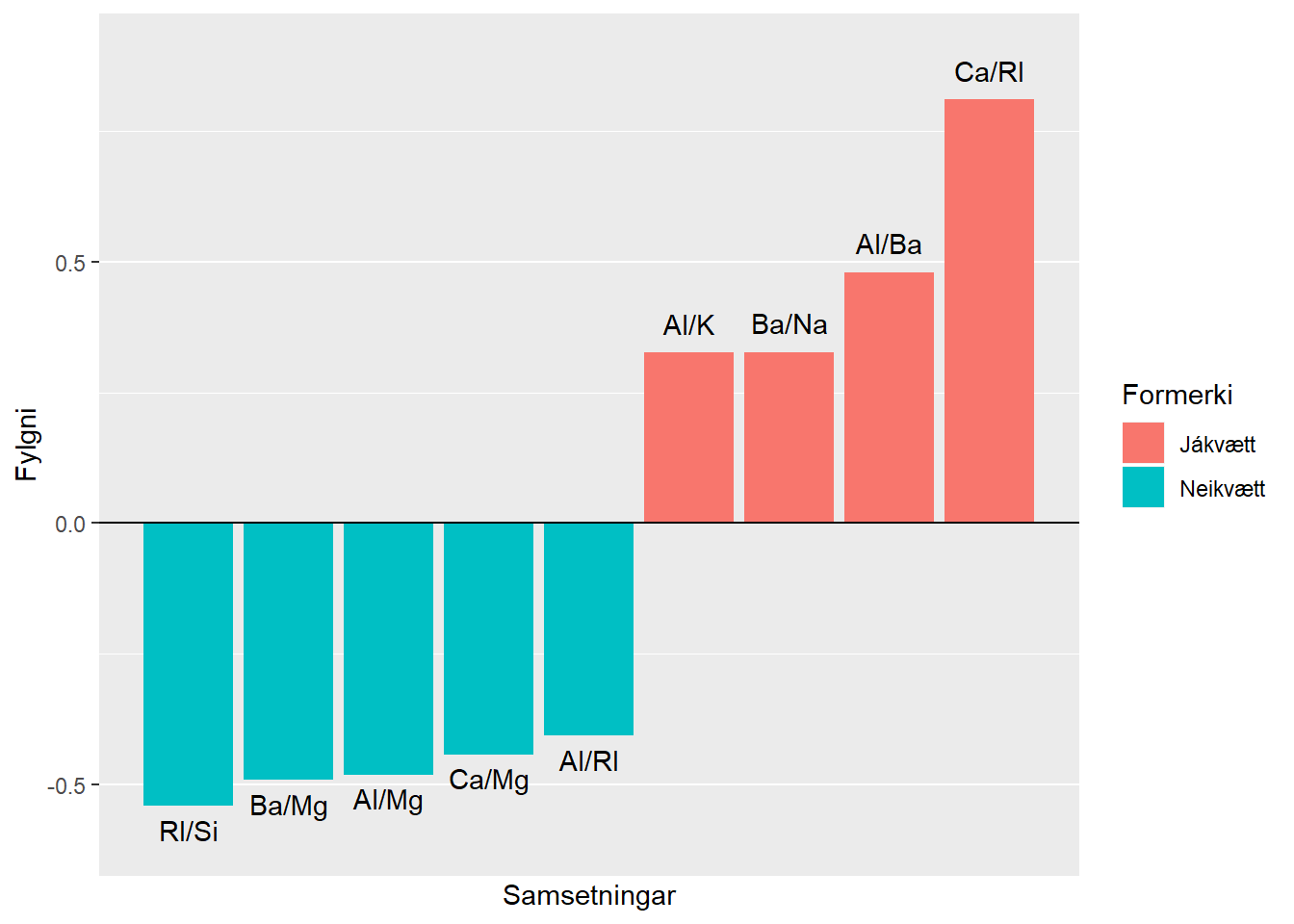
Þá sjáum við að ef að við notum ljósbrotsstuðul RI sem skýribreytu fyrir tegund glersins, þá er efnið Ca að fara að veita okkur minnstar viðbótarupplýsingar, og öfugt. Eins og ég nefndi hér að ofan getur marglínuleiki valdið okkur vandræðum. Þannig væri líklega okkar fyrsta verk að fjarlægja ljósbrotsstuðulinn RI, þar sem sterk fylgni er milli hans og efnisins Ca, og jafnframt tiltölulega sterk neikvæð fylgni milli hans og efnisins Si. Það væri þá til að koma í veg fyrir marglínuleika fyrir þau líkön sem slíkt hefur áhrif á, en ef til vill væri það líka eftirsóknarvert til einföldunar þó að við værum með til dæmis slembiskógalíkan, sem marglínuleiki hefur ekki áhrif á. Það að fækka skýribreytum einfaldar líkanið og styttir reiknitíma. Að því sögðu þá er fókusinn í þessu dæmi á forvinnsluaðgerðir til að leiðrétta fyrir skekkingu í dreifingu5 - þannig við látum það ógert að henda út ljósbrotsstuðlinum að svo stöddu.
Forvinnsluaðgerðir
Til að leiðrétta fyrir skekkingu í dreifingu
Til að leiðrétta fyrir skekkingu í dreifingu skýribreytanna væri ákjósanlegt að geta beitt fyrir sig Box-Cox umbreytingu. Til þess þurfa öll gildi að vera stærri en núll. Því þurfum við að athuga hvort einhver núllgildi eða neikvæð gildi leynist í einhverjum skýribreytanna. Til þess að auðvelda okkur það erum við sniðug og notumst við map_dbl() fallið úr purrr pakkanum. Við höfum þegar hlaðið inn purrr hér að ofan um leið og við hlóðum inn tidyverse pakkasamstæðunni.
Glass[, skyribreytur] %>%
map_dbl(~sum(. <= 0))## RI Na Mg Al Si K Ca Ba Fe
## 0 0 42 0 0 30 0 176 144Einungis RI, Na, Al, Si og Ca innihalda bara jákvæð gildi, en hin ekki. Við sjáum því strax að Box-Cox umbreyting er ekki valkostur fyrir allar skýribreyturnar, né þá heldur log-umbreyting. Þá prófum við Yeo-Johnson umbreytingu, en hún er ekki alls ósvipuð Box-Cox nema fyrir það að gildi mega vera neikvæð eða núll. Raunar er Yeo-Johnson umbreytingin í reynd Box-Cox umbreyting í þeim tilfellum þar sem öll gildi breytu eru jákvæð. Til þess að kalla fram Yeo-Johnson umbreytingu getum við notað preProcess() fallið úr caret pakkanum, sem skrifaður er af Max Kuhn, öðrum höfundi Applied Predictive Modeling sem verkefnið er úr.
Við ætlum einnig að prófa að miðja og skala gögnin.
pp_object_Glass_both <- preProcess(Glass, method = c("center", "scale", "YeoJohnson"))
glass_both <- predict(pp_object_Glass_both, Glass)
pp_object_Glass_yj <- preProcess(Glass, method = c("YeoJohnson"))
glass_yj <- predict(pp_object_Glass_yj, Glass)
pp_object_Glass_cs <- preProcess(Glass, method = c("center", "scale"))
glass_cs <- predict(pp_object_Glass_cs, Glass)Prófum sambærilegt þéttnirit og áður. Berum saman tvær mismunandi uppskriftir að forvinnslu. Annars vegar miðjun og skölun, og hins vegar miðjun, skölun og Yeo-Johnson umbreytingu. Hér er búið að kommenta út þrjú önnur þéttnirit, svo þau birtist ekki.
# glass_both %>%
# gather(-Type, key = "efni", value = "gildi") %>%
# ggplot(mapping = aes(x = gildi)) +
# geom_density() +
# facet_wrap(~efni, scales = "free")
#
#
# glass_yj %>%
# gather(-Type, key = "efni", value = "gildi") %>%
# ggplot(mapping = aes(x = gildi)) +
# geom_density() +
# facet_wrap(~efni, scales = "free")
#
# glass_cs %>%
# gather(-Type, key = "efni", value = "gildi") %>%
# ggplot(mapping = aes(x = gildi)) +
# geom_density() +
# facet_wrap(~efni, scales = "free")
glass_both_tidy <- glass_both %>%
gather(-Type, key = "efni", value = "gildi")
glass_cs_tidy <- glass_cs %>%
gather(-Type, key = "efni", value = "gildi")
glass_saman <- bind_rows("Fyrir" = glass_cs_tidy, "Eftir" = glass_both_tidy, .id = "Y-J umbreyting")
glass_saman %>%
ggplot(mapping = aes(x = gildi, color = `Y-J umbreyting`, fill = `Y-J umbreyting`)) +
geom_density(alpha = 0.2) +
facet_wrap(~efni, scales = "free")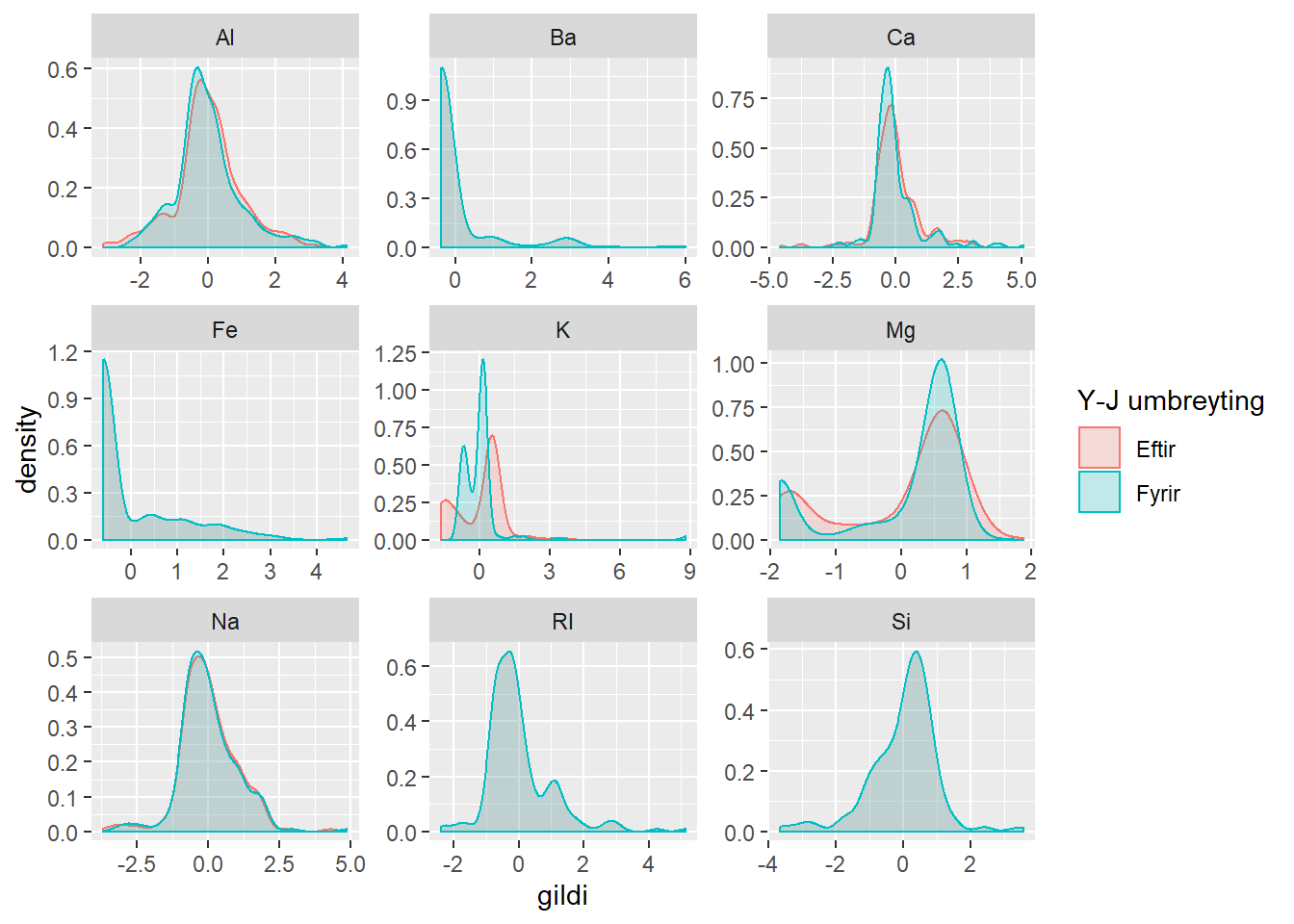
Eru forvinnsluaðgerðirnar líklegar til að bæta spár um flokkun glersins?
Til þess að svara því liggur beinast við að forvinna gögnin eftir mismunandi uppskriftum og spá því næst fyrir um tegundir glers út frá skýribreytunum. Við búum til þjálfunarsett og prófunarsett til að vinna með. training_set_raw og test_set_raw eru grunngögnin án nokkurar forvinnslu. Í training_set_cs og test_set_cs eru gögnin miðjuð og sköluð6. Í training_set_yj og test_set_yj er notast er við Yeo-Johnson umbreytingu. Í training_set_both og test_set_both er notast við miðjun og skölun, og Yeo-Johnson umbreytingu.
Við tökum 85% af gögnunum og notum þau sem þjálfunarsett og restin verður prófunarsett.
train_ind <- caret::createDataPartition(y = glass_cs$Type, p = 0.85, list = FALSE)
pred_vars <- 1:9 # Dálkanúmer skýribreytanna
training_set_raw <- Glass[train_ind, ]
training_set_both <- glass_both[train_ind, ]
training_set_cs <- glass_cs[train_ind, ]
training_set_yj <- glass_yj[train_ind, ]
test_set_raw <- Glass[-train_ind, ]
test_set_both <- glass_both[-train_ind, ]
test_set_cs <- glass_cs[-train_ind, ]
test_set_yj <- glass_yj[-train_ind, ]Þegar við höfum skilgreint þjálfunarsett og prófunarsett hefjumst við handa við að þjálfa líkanið á hráu, óunnu gögnunum. Við notumst við caret pakkann, en hann er samansafn tóla til spálíkanagerðar. Við notumst einnig við caretEnsemble pakkann, sem er allajafna notaður til að búa til samleik spálíkana. Með samleik er átt við það að búa til eitt líkan úr mörgum líkönum til að bæta spánákvæmni. Hér ætlum við hinsvegar einungis að nota hann til að halda utan um mismunandi reiknirit sem við ætlum að beita á gögnin. knn er næsta-nágranna reiknirit7, treebag er bagged trees reiknirit, rf er slembiskógur8, rpart er einfalt ákvarðanatré9, svmRadial er stuðningsvigra reiknirit með kúlulaga ákvörðunarskilum10. xgbTree aðferðin kallar til xgboost reikniritið sem framkvæmir ofurmögnun stiguls11.
Við notumst við 3 sinnum 10 brota kross prófun12 í öllum tilvikum til að reyna að tryggja að við séum ekki að ofsníða13 að þjálfunargögnunum.
styring_reiknirita <- trainControl(method="repeatedcv", number=10, repeats=3, index = createMultiFolds(training_set_raw$Type, k = 10, times = 3),
savePredictions="final", classProbs=TRUE)
listi_reiknirita <- c('knn', 'treebag', 'rf', 'rpart', 'svmRadial', 'xgbTree') Hér nota ég 7 kjarna til að skipta útreikningunum niður á. Ef þú hyggst keyra þessa útreikninga á eigin vélbúnaði þarf að taka mið af fjölda kjarna í örgjörva vélbúnaðarins sem útreikningarnir fara fram á. Að því sögðu er vert að nefna að formúluviðmótið hægir talsvert á útreikningum á xgboost, þannig í raun væri vond hugmynd að kópera þennan kóða beint. En hey, ég er búinn að þjálfa líkönin þegar þessi orð eru skrifuð, þannig það skiptir ekki öllu máli.
training_set_raw$Type <- as.factor(training_set_raw$Type)
levels(training_set_raw$Type) <- c("One", "Two", "Three", "Five", "Six", "Seven")
cl <- makeCluster(7)
registerDoParallel(cl)
models_raw <- caretList(Type ~ ., data = training_set_raw,
trControl = styring_reiknirita,
methodList = listi_reiknirita)
results_raw <- resamples(models_raw)
stopCluster(cl)Því næst gerum við hið nákvæmlega sama fyrir gagnasettið sem hefur verið skalað og miðjað.
training_set_cs$Type <- as.factor(training_set_cs$Type)
levels(training_set_cs$Type) <- c("One", "Two", "Three", "Five", "Six", "Seven")
cl <- makeCluster(7)
registerDoParallel(cl)
models_cs <- caretList(Type~., data=training_set_cs,
trControl = styring_reiknirita,
methodList = listi_reiknirita)
results_cs <- resamples(models_cs)
stopCluster(cl)Og því næst gagnasettið með Yeo-Johnson umbreytingu.
training_set_yj$Type <- as.factor(training_set_yj$Type)
levels(training_set_yj$Type) <- c("One", "Two", "Three", "Five", "Six", "Seven")
cl <- makeCluster(7)
registerDoParallel(cl)
models_yj <- caretList(Type~., data=training_set_yj,
trControl = styring_reiknirita,
methodList = listi_reiknirita)
results_yj <- resamples(models_yj)
stopCluster(cl)Og svo fyrir gögnin með miðjun og skölun, og Yeo-Johnson umbreytingu.
training_set_both$Type <- as.factor(training_set_both$Type)
levels(training_set_both$Type) <- c("One", "Two", "Three", "Five", "Six", "Seven")
cl <- makeCluster(7)
registerDoParallel(cl)
models_both <- caretList(Type~., data=training_set_both,
trControl = styring_reiknirita,
methodList = listi_reiknirita)
results_both <- resamples(models_both)
stopCluster(cl)Þegar við höfum þjálfað áðurnefnd líkön á gögnum með mismunandi ‘forvinnslu-uppskriftum’ skoðum við áhrif forvinnslu á spánákvæmni. Í stað þess að nota bara nákæmni14 (hlutfall þeirra athugana sem líkan flokkar rétt) heldur skoðum við einnig Cohen’s Kappa, sem er mælikvarði á nákvæmni líkansins umfram vænta nákvæmni. Þá er átt við að í tilvikum þar sem eru einungis tveir flokkar má vænta að slembiflokkari myndi flokka athugun í réttan flokk í helmingi tilvika.
Cohen’s kappa er reiknað á eftirfarandi hátt.
nidurstodur <- list("hrátt" = results_raw$values,
"cs" = results_cs$values,
"yj" = results_yj$values,
"bæði" = results_both$values) %>%
map(~as_tibble(.)) %>%
map(~set_names(., ~str_replace(., "~", "_"))) %>%
bind_rows(.id = "pre_process") %>%
group_by(pre_process) %>%
summarize_at(.vars = vars(-1),
.funs = mean) %>%
pivot_longer(-pre_process, names_to = "model_metric", values_to = "value") %>%
arrange(model_metric, pre_process) %>%
separate(col = model_metric, into = c("model", "metric"), sep = "_") %>%
mutate(pre_process = fct_relevel(pre_process, "hrátt", "cs", "yj", "bæði"))
nidurstodur %>%
filter(metric == "Kappa") %>%
ggplot(aes(x = pre_process, y = value, fill = pre_process)) +
geom_col() +
facet_wrap(~model) +
labs(title = "Cohen's Kappa eftir forvinnsluaðferð")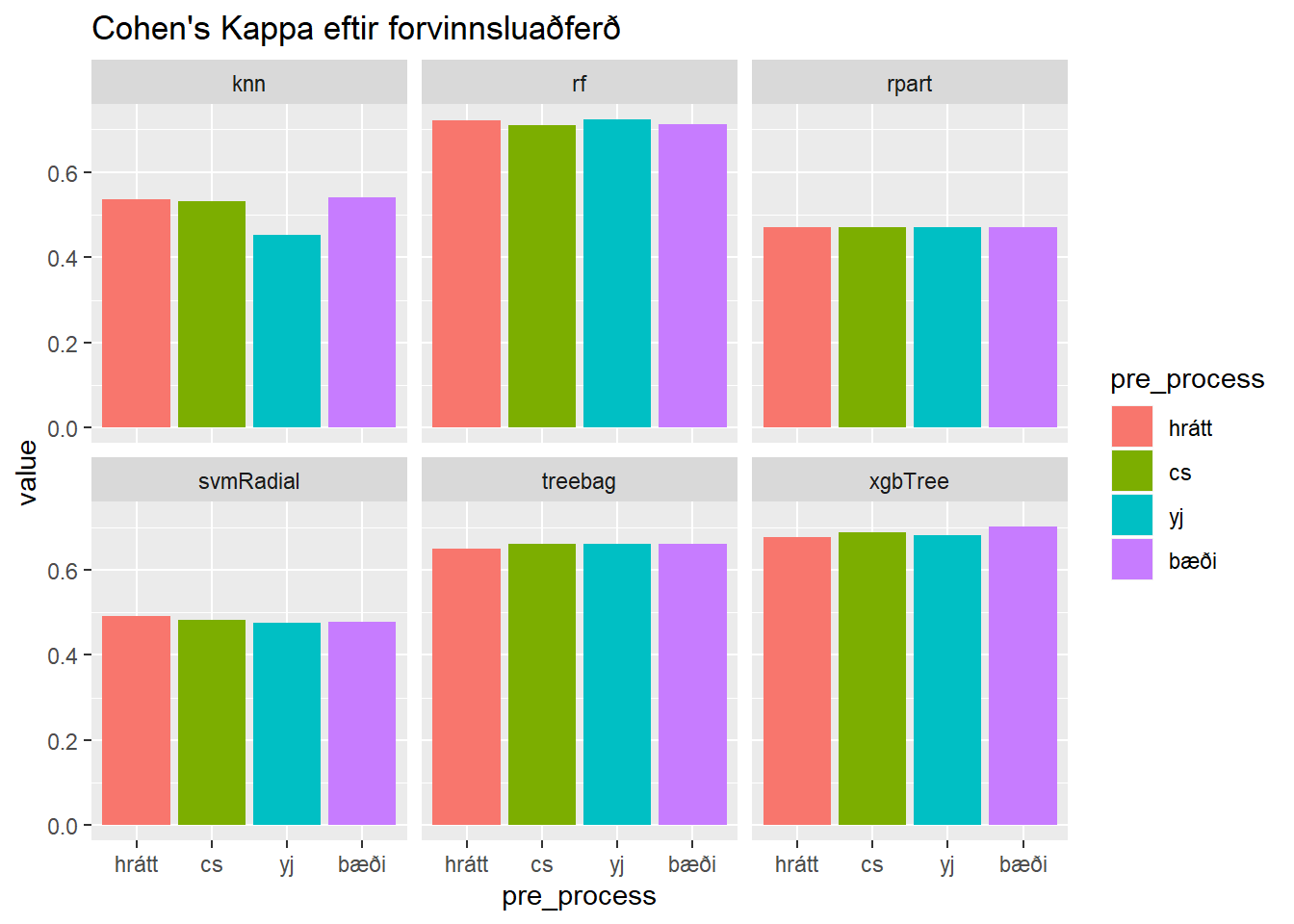
nidurstodur %>%
filter(metric == "Accuracy") %>%
ggplot(aes(x = pre_process, y = value, fill = pre_process)) +
geom_col() +
facet_wrap(~model) +
labs(title = "Nákvæmni eftir forvinnsluaðferð")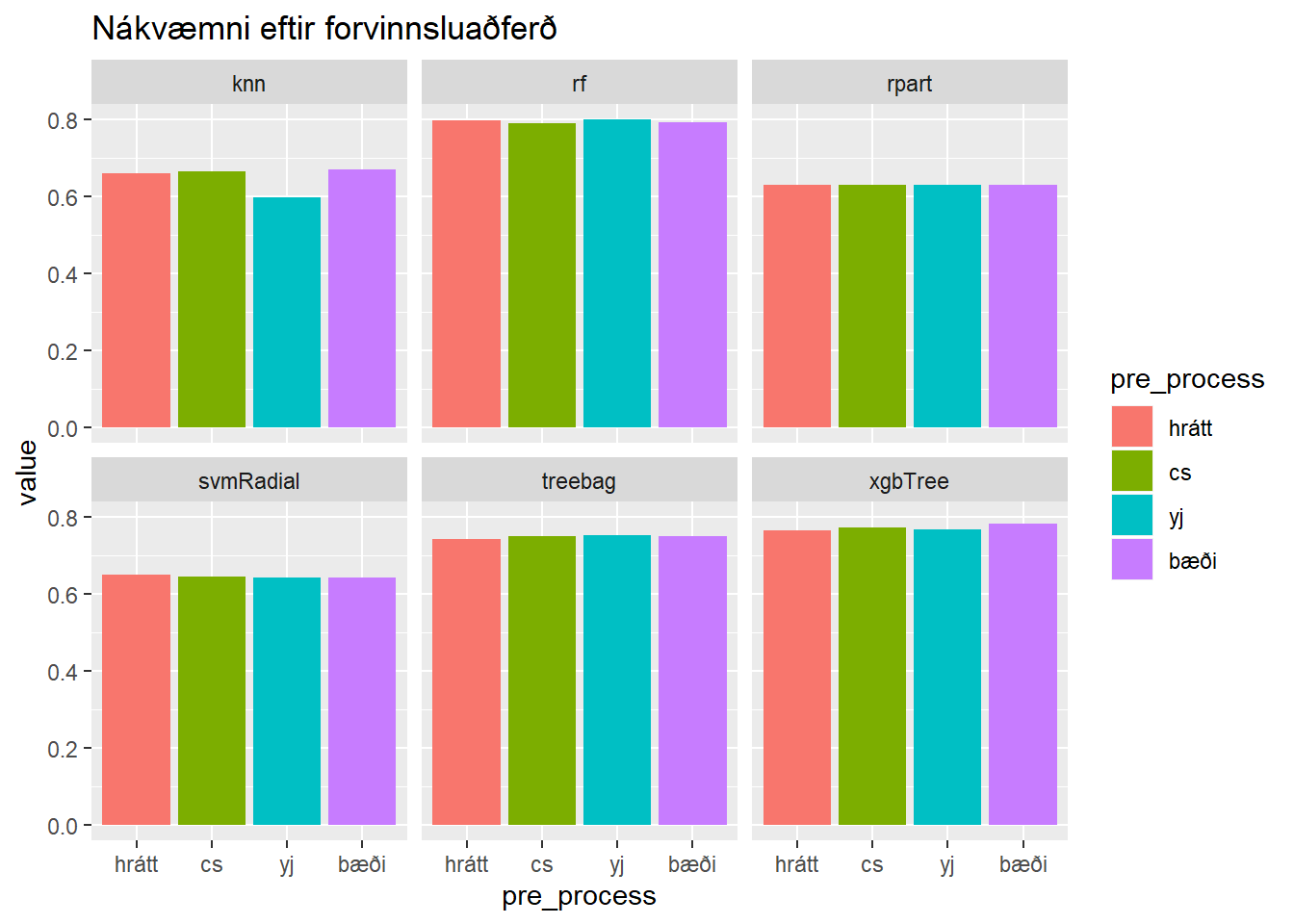
nidurstodur %>%
filter(metric == "Accuracy") %>%
group_by(model) %>%
mutate(centered = value - mean(value)) %>%
ggplot(aes(x = pre_process, y = centered, fill = pre_process)) +
geom_hline(yintercept = 0) +
geom_col() +
facet_wrap(~model) +
labs(title = "Frávik frá meðalnákvæmni hvers reiknirits")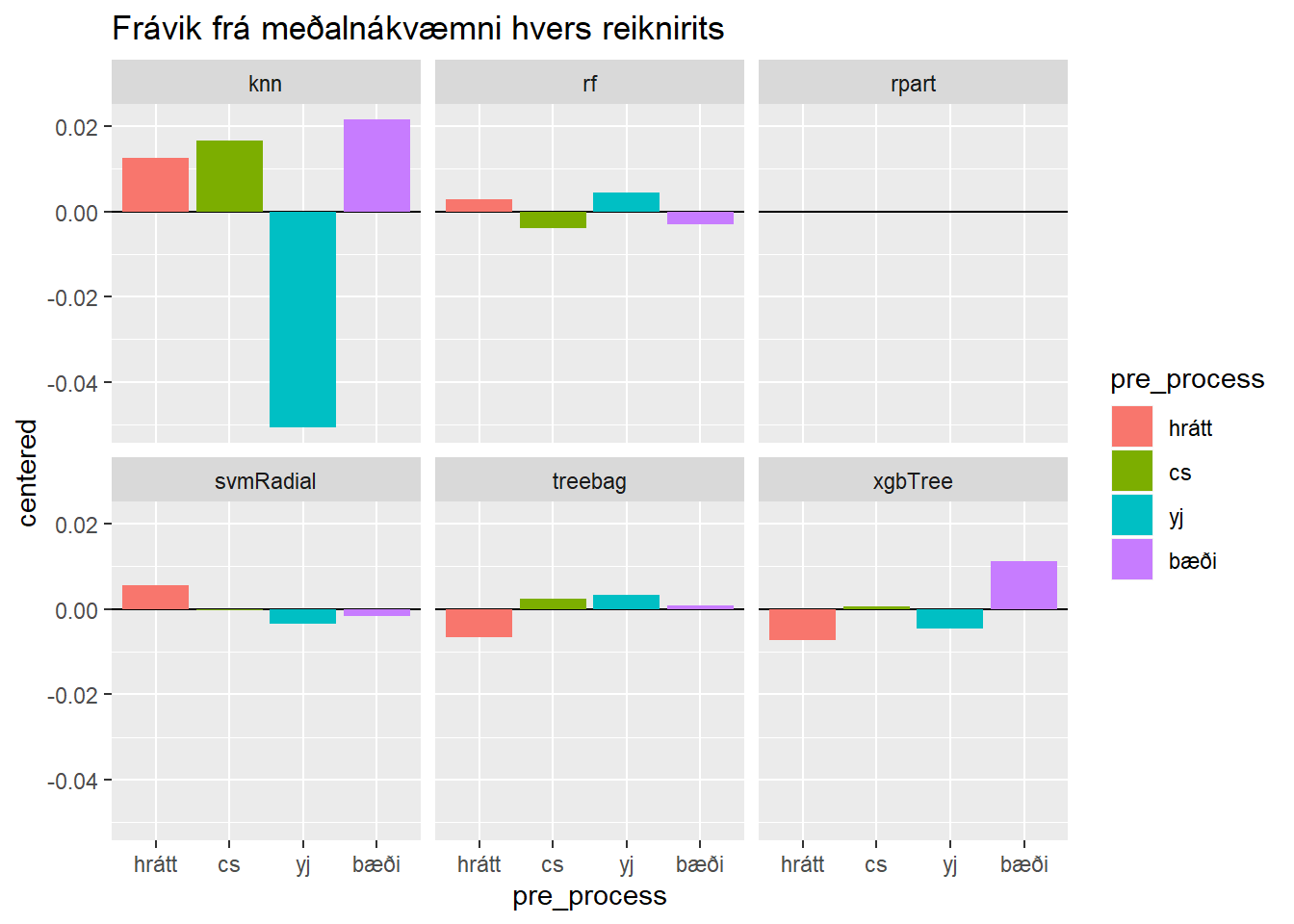
Þannig sjáum við að slembiskógareikniritið rf skilar besta líkaninu fyrir okkur. Við sjáum jafnframt að sú forvinnsluaðferð sem skilar besta slembiskógalíkaninu er Yeo-Johnson umbreyting án miðjunar og skölunar.
nidurstodur %>%
filter(value == max(value))## # A tibble: 1 x 4
## pre_process model metric value
## <fct> <chr> <chr> <dbl>
## 1 yj rf Accuracy 0.799Nákvæmni slembiskógalíkansins með Yeo-Johnson umbreytingu er 79.9% á þjálfunargögnunum. Það eru séð gögn.
models_yj$rf## Random Forest
##
## 185 samples
## 9 predictor
## 6 classes: 'One', 'Two', 'Three', 'Five', 'Six', 'Seven'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold, repeated 3 times)
## Summary of sample sizes: 168, 168, 167, 168, 166, 166, ...
## Resampling results across tuning parameters:
##
## mtry Accuracy Kappa
## 2 0.7990341 0.7234367
## 5 0.7684922 0.6854291
## 9 0.7491762 0.6602136
##
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was mtry = 2.Við sjáum að bakvið tjöldin valdi caret gildið 2 fyrir stillibreytuna15 mtry, sem stjórnar fjölda þeirra breyta sem eru mögulegar í slembivali sem kandidatar fyrir “splitt” í ákvarðanatrjánum sem liggja að baki slembiskógalíkaninu. Við sjáum einnig að caret hefur skoðað þrjú möguleg gildi fyrir mtry.
Framhaldið
Við erum búin að komast að því að slembiskógur hentar vel fyrir þessi gögn, og þessi æfing gefur til kynna að það sé best að beita bara Yeo-Johnson umbreytingu á gögnin. Í raun er þó ótrúlega lítill munur á nákvæmninni milli forvinnsluaðgerða, þannig það er strangt til tekið ekkert útséð í þeim málum.
Ef þetta væri raunverulegt verkefni myndum við nú halda áfram og einblína á þau líkön sem koma best út. Til dæmis að einblína á slembiskógalíkön, en gefa caret leiðbeiningar um að skoða fleiri gildi fyrir stillibreytuna mtry og sjá hvort það geti ekki haft þónokkur áhrif.
Þegar við værum orðin sátt við nákvæmnina á séðum gögnum út frá tiltekinni nálgun myndum við því næst reikna nákvæmni og Kappa fyrir óséð gögn. Það eru gögn sem voru ekki notuð til að þjálfa líkanið. Til þess erum við með prófunarsett. Við myndum mæla nákvæmni og Kappa á prófunarsettinu og niðurstaðan úr því væri sú nákvæmni sem við gætum búist við af líkaninu.
Að lokum er vert að koma eftirfarandi fyrirvara að: Í þessu vandamáli hefur nálgunin alfarið verið reiknidrifin16 og að engu leyti reynsludrifin17. Ég hef enga sérfræðiþekkingu eða reynslu sem snýr að flokkun mismunandi gerða glers sem hefði getað nýst mér í þessu verkefni. Í raunveruleikanum þarf maður að prjóna saman sérfræðiþekkingu við tölfræðilega útreikninga til þess að ná sem bestum árangri. En það er efni í annað blogg.
Takk í dag!
(e. supervised machine learning)↩
(e. regression problem)↩
(e. classification problem)↩
(e. pre-processing)↩
(lesist: ég sjúklega latur og þetta er bara sýnidæmi)↩
(e. centering and scaling)↩
(e. nearest neighbour)↩
(e. random forest)↩
(e. decision tree)↩
(e. support vector machines using a radial decision boundary)↩
(e. extreme gradient boosting)↩
(e. cross-validation)↩
(e. over-fit)↩
(e. accuracy)↩
(e. tuning parameter)↩
(e. empirically driven modeling)↩
(e. experience-driven modeling)↩